|
The ISP Column
A column on things Internet
|
|
|
|
|

November 2011
Geoff Huston
Whenever this discussion about routing growth and scalability takes place, there is a related discussion about what aspect of scaling is being discussed. Is it really the size of the routing space that is the topic of abiding concern, or is it the dynamic properties of the routing system? Should we be looking at the volume of BGP update messages per unit time? Or perhaps we might look at the average time to reach convergence? More generally, are there metrics relating to the dynamic behavior of the routing protocol itself that may be a cause for concern about the scalability of the Internet's routing system?
In attempting to address these questions I have used a data set that includes every BGP update over a period of several years at AS 131072. Before examining the data I should note the circumstances this AS. It lies at the edge of the network, and does not provide transit to any other network. Secondly, it is a single LAN, so there is no internal routing protocol, nor any iBGP within the network. Thirdly, the data collected and analyzed here relates to a single eBGP session. So what we are examining here is a pretty typical edge network's eBGP feed that has been stable over an extended period of time.
Counting BGP Updates
The figure below shows the number of BGP updates per day, or to be more precise, the number of prefix updates per day since mid 2007 in IPv4. To clarify this measurement, I should note that this is not exactly the same as the number of BGP protocol messages received by the AS131072 router. The measurement reflects the number of times each prefix is updated per day, where each "update" is either a withdrawal or an announcement. This data is shown in Figure 1.
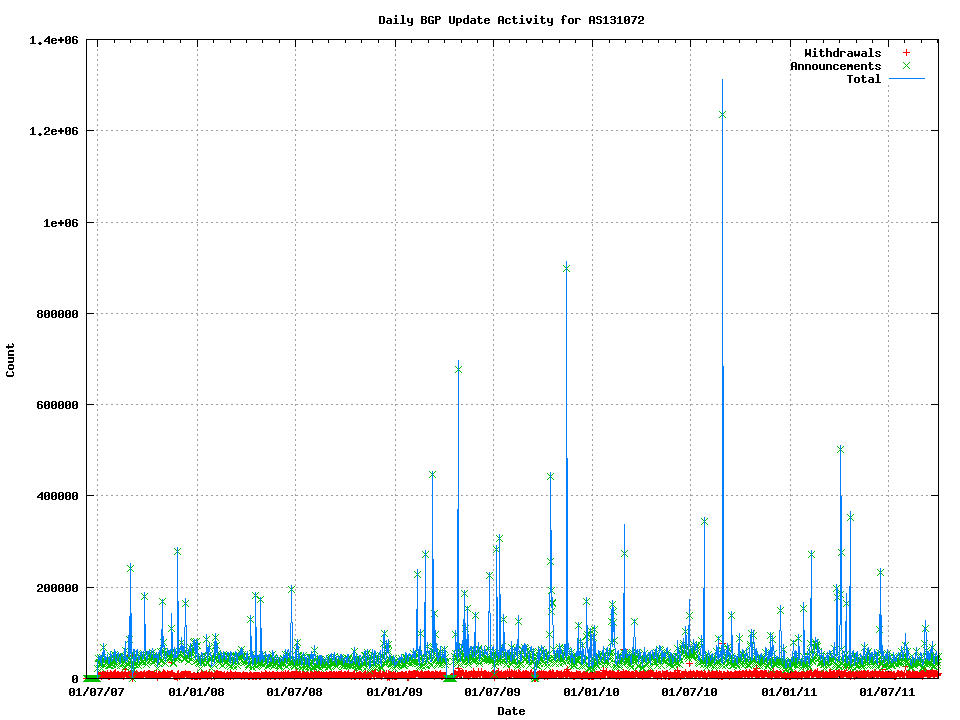
Figure 1 - Daily BGP Updated Prefix Counts for 2007 - 2011
The daily withdrawal rate has been relatively constant, while the number of updates per day shows a number of outlier days with prefix update volumes between 100,000 to 1,000,000 prefix updates.
These high volume outlier days are attributable to BGP session resets close to the BGP measurement system, where a nearby BGP system performs a session reset and is re-fed the complete route set. On some occasions there were multiple resets in the day, including one day where the BGP table was reloaded 9 times. These local session reset updates can be filtered out from the data set.
Announcements
A filtered view of the number of prefix announcements per day is shown in Figure 2 This figure also includes a least squares best fit to the data set, which produces a model of the growth of the number of updates per day as follows:
Updates = (-233.8584 * year) - 511403.5
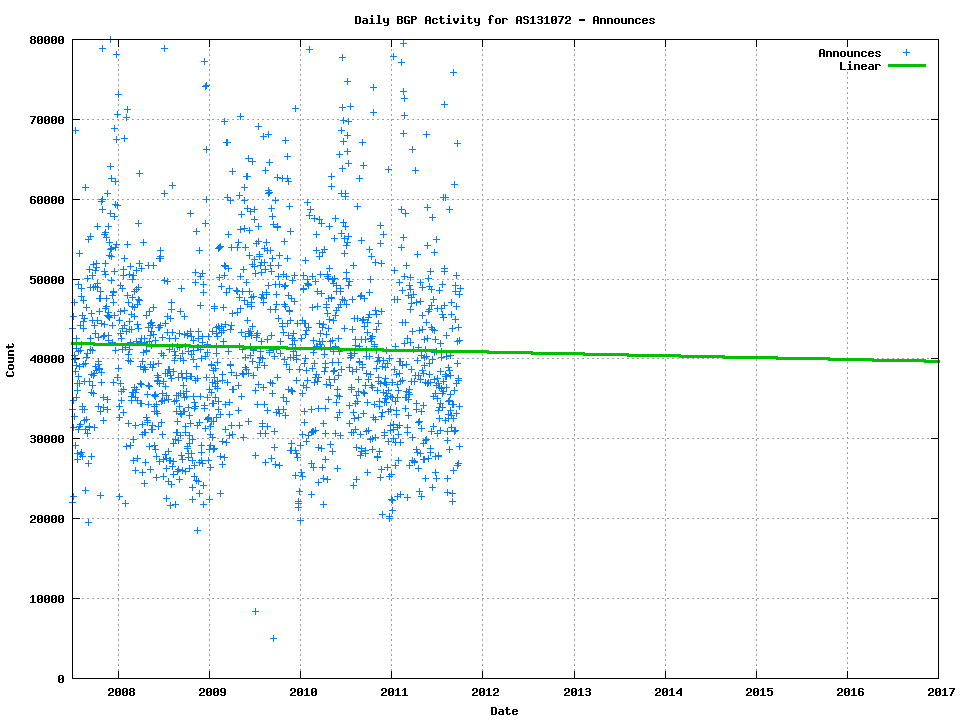
Figure 2 -Daily BGP Prefix announcements for 2007 - 2011
This data shows a daily rate of some 40,000 updated prefixes per day, or an average prefix update rate at a level of around 1 updated prefix every 2 seconds. Obviously this average announcement rate has very little relationship to the peak update rate that a BGP speaker is likely to see (which would conventionally be anticipated when the local BGP speaker comes up and all its’ eBGP peers provide a complete route set at wire speed) , but this daily average update rate is a useful metric in looking at the order of scale of the processing load imposed by the flow of eBGP updates.
The announcement data shows a surprisingly consistent view of BGP updates with a negative growth projected in the coming years, based on the data from previous years. If there is a looming issue with BGP update processing loads in the coming years, the rate of eBGP updates (excluding those that are unrelated to local BGP session resets) does not appear to be a strong contributor to any such issue.
Withdrawals
A subtly different story is visible in the withdrawal data. The daily count of withdrawals over 2007 - 11 is shown in Figure 3, including a linear projection into the coming years using the model:
Withdrawals = 472.5620 * year - 941571.8
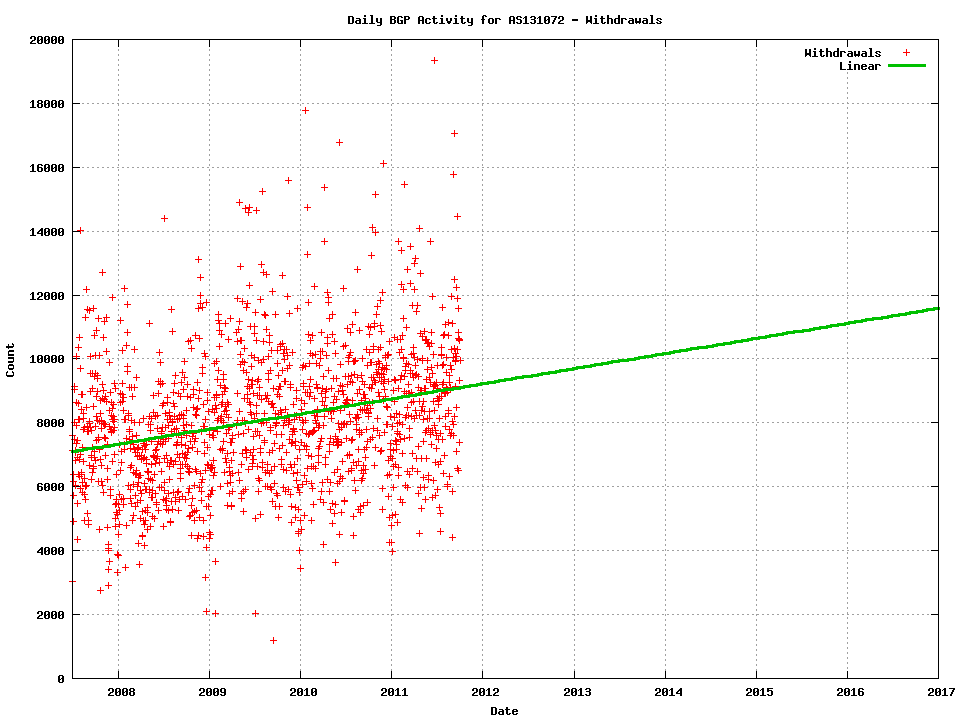
Figure 3 -Daily BGP Prefix withdrawals for 2007 - 2011
Here a growth trend is visible, but in absolute terms a growth of the number of withdrawals per day from the current average of some 9,000 withdrawals per day to slightly less that 12,000 withdrawals per day over the coming five years is once again not a major cause for concern in terms of growth pressures and scaling BGP.
Table Size
These figures should be compared to the size of the BGP table, which is growing at a rate which is approximately 10% per year. A curve fit to the BGP Table data provides the model:
Routing Entries = 500.8477 year2 - 1978271 year + 500.8477
The ratio of the announce and withdrawal volumes to the BGP table size model is shown in Figure 4.
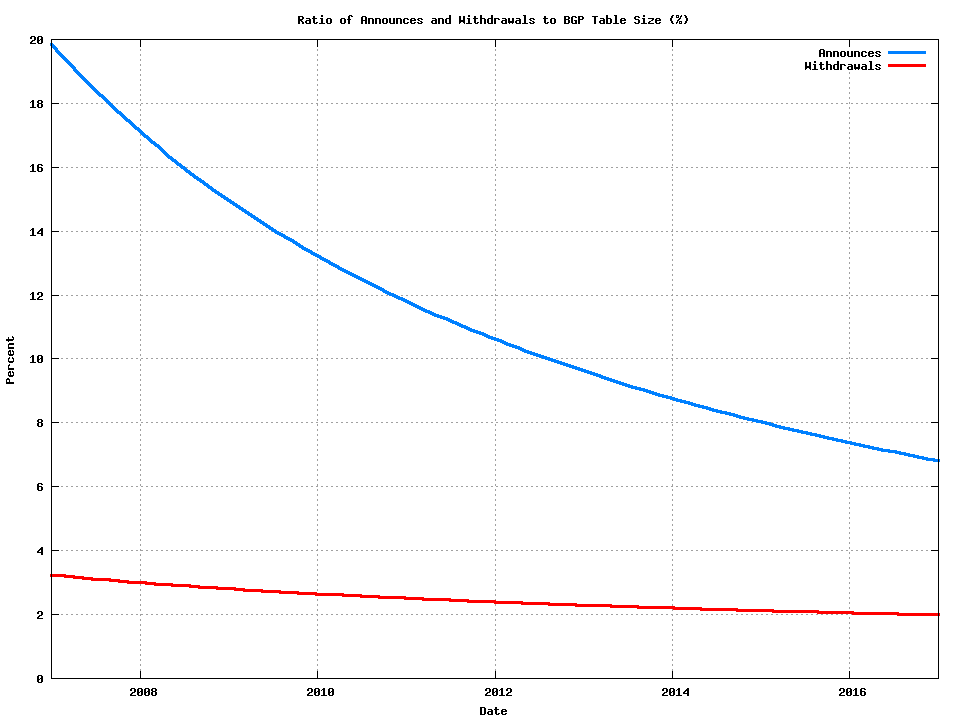
Figure 4 – Ratio of Announce and Withdrawals to BGP Table Size: 2007 - 2017
What is evident is that over time the level of protocol activity of routing, as measured by the eBGP update volume, is declining, as compared to the total population of such routed objects. Why is this projected growth rate for prefix updates so much smaller than the projections for the growth in the BGP table size?
Counting Unstable Prefixes
Surely a more richly connected, larger routing space would generate more routing protocol update traffic. Wouldn't there be more prefixes that are the subject of BGP updates each day as the number of routed entries increases in size? Even if one takes a more conservative view, and rather than assuming that the probability of a prefix being the subject of a routing change is uniformly constant, assume that each origin AS is equally likely to generate routing updates, then that model also would infer that the number of unstable prefixes grows in proportion to the number of Ass described in the entire routing system.
Figure 5 shows the number of prefixes that are the subject of updates each day. This is independent of the intensity of the number of updates seen for any particular prefix on that day, and simply counts the number of unstable prefixes per day. What is notable here is the bi-modal nature of this data set. The upper part in Figure 5 is the total number of prefixes in the routing table over the period 2007 to October 2011, and that sub-sequence in the data reflects those days that experienced a nearby BGP peer reset of some form or another that resulted in all the prefixes in the BGP routing table being updated on that day. The lower collection of data is a set of prefixes that are updated each day that appear to to be relatively steady is size for many years.
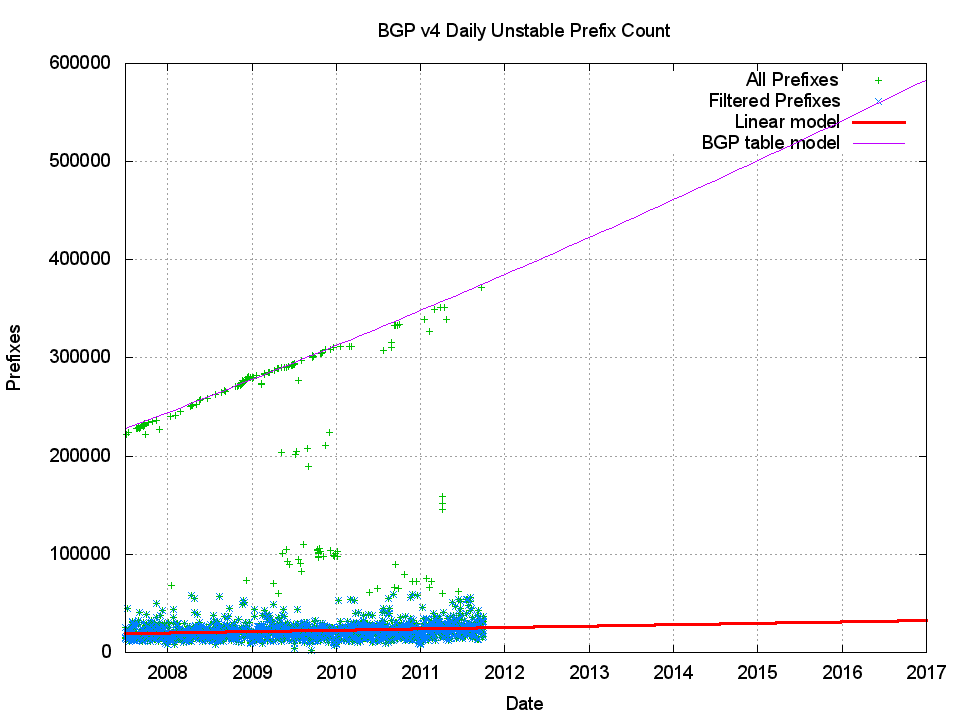
Figure 5 - Daily count of the number of updated prefixes per day
This is a very surprising outcome. BGP routing table has grown from some 220,000 entries in July 2007 to some 380,000 entries in October 2011, or a relative size difference of 73%. But at the same time the number of unstable prefixes per day has grown extremely slowly. At the start of 2008 there were an average of 19,843 unstable prefixes per day (+/- some 10,000 prefixes), and by the start of 2012 there are projected to be 25,472 unstable prefixes per day. The comparable growth in the average number of unstable prefixes over the same period is 25%, or one third of the growth in the number of prefixes in the routing table.
Not only is the average number of unstable prefixes growing at a slower rate than the number of prefixes, but the number of withdrawals and updates is also growing at a slower rate than the routing table as well. Again, this appears to be a surprising result, in that it would be reasonable to expect that an instance of prefix instability would generate more protocol updates as a result of BGP's distance vector algorithm attempting to reach convergence across a denser and more richly interconnected network topology. And wouldn't it be reasonable to expect that the interaction between a larger routing space and the Minimum Router Advertisement Interval (MRAI) default timer settings on propagation of withdrawals in commonly deployed routing equipment work to extend convergence times as the network itself grew?
One way of looking at this is to look at the average number of BGP updates required to reach a converged, or stable, routing state, and the average amount of time taken for routing to reach convergence. Here a "convergence event" is defined as a sequence of 1 or more updates for the same prefix separated by no more that 135 seconds, and "stability" is defined as no further updates for 135 seconds or longer.
The following figure (Figure 6) shows the number of 'instability events' where a prefix took one or more updates before reaching a converged state. The following two figures (Figure 7 and Figure 8) show the daily average of the number of updates seen before a prefix is considered stable, and the average amount of time taken for the entire sequence of updates. BGP is a distance vector protocol and state changes further "away" from the listening point are likely to to generate a higher number of routing protocol updates before converging to a stable state, while a local event, such as a peer BGP speaker reset, will generate a table reload where each prefix is updated in a single protocol notification. To try and gain a basic picture of the difference between the two categories of instability, "near" and "far", the following figures also show the metrics for convergence sequences which have a minimum of 2 updates, as well as the entire set of convergence sequences.
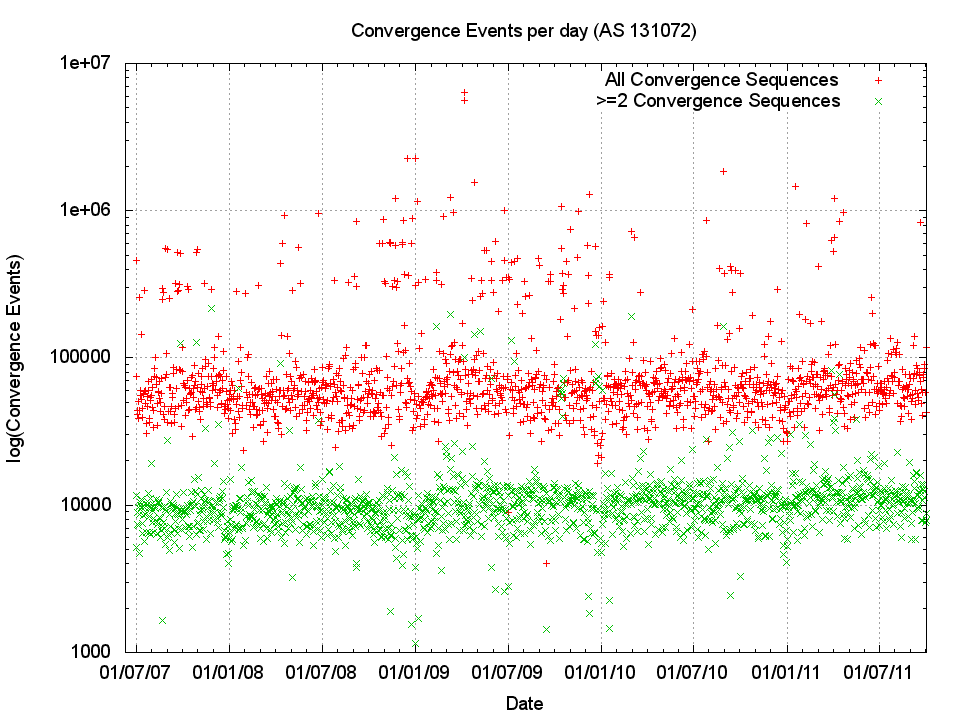
Figure 6 – BGP Convergence Events per Day
The trend in the number of these 'instability' events appears to be relatively constant on a daily basis. In other words the network as a whole appears to be no more or less unstable now as it was in 2007, with around 60,000 ± 20,000 such convergence events per day, and 10,000 events per day that require 2 or more updates to converge to stability. Figures 7 and 8 similarly illustrate that the trends of average daily convergence sequence length and duration are not changing over time, but have ben extremely steady over time.
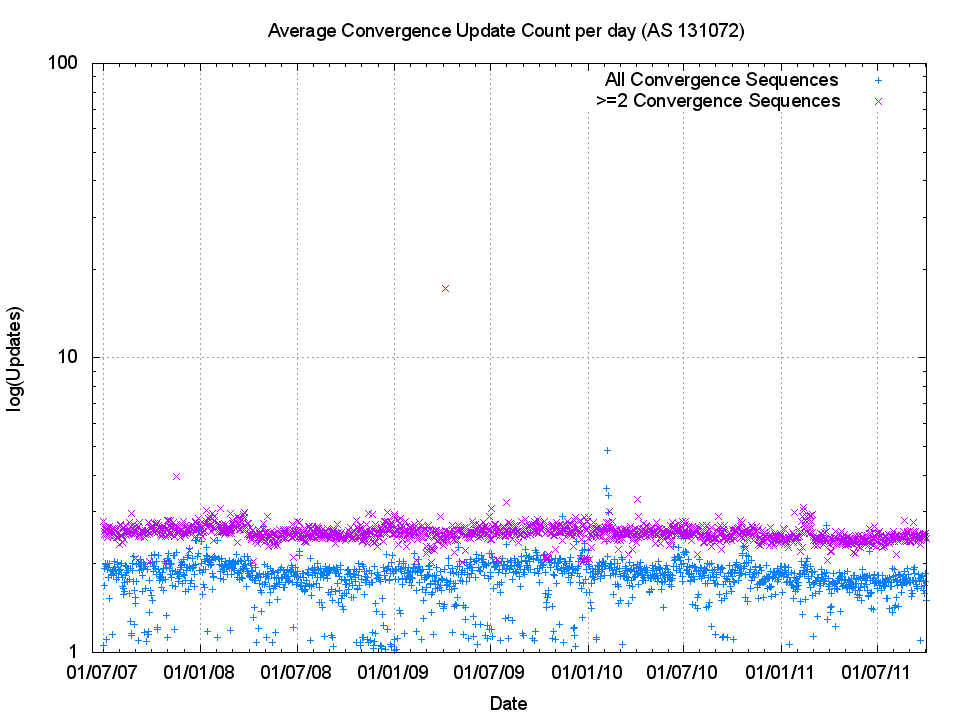
Figure 7 -Daily Average of BGP Updates to reach convergence
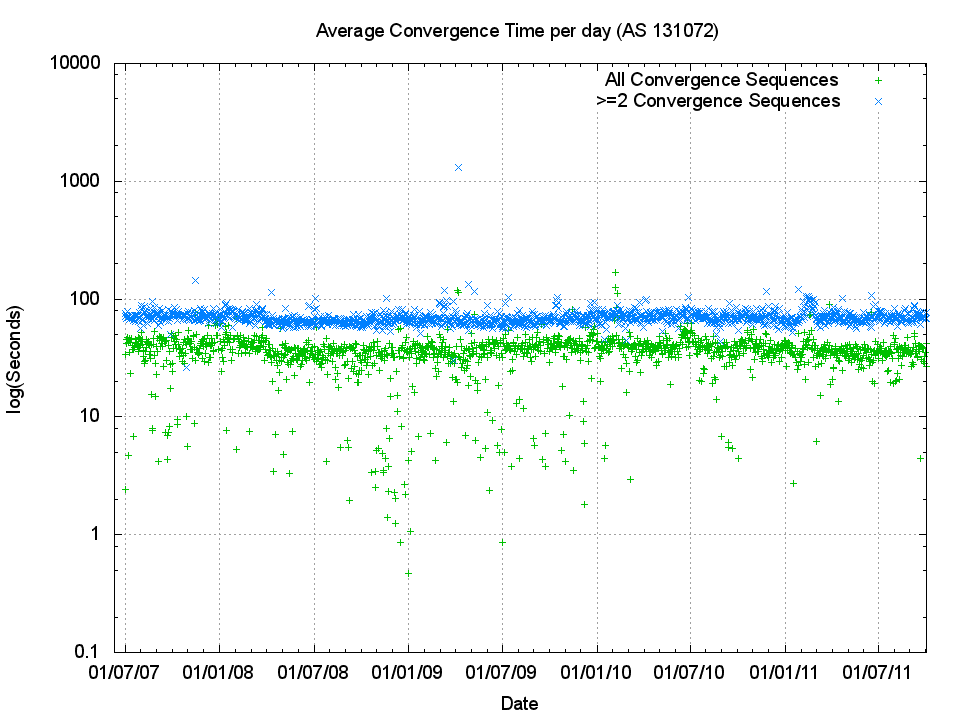
Figure 8 - Daily Average of elapsed seconds to reach convergence
What can we say about these unstable prefixes?
Is it the same set of prefixes that are unstable each and every day on a very long term basis? This situation would be expected if there is use of routing to perform traffic engineering on a fine-grained basis, where each day the same core set of more specific routes are moved between upstream providers in order to manipulate the relative balance of incoming traffic on nodes.
The other possibility is that the set of unstable prefixes vary each day. This would imply that the basis for their instability is perhaps related to some aspect of the network's topology, or some observations relating to trends in basic circuit stability where growth in the routing space is offset by general ongoing improvements in network infrastructure stability.
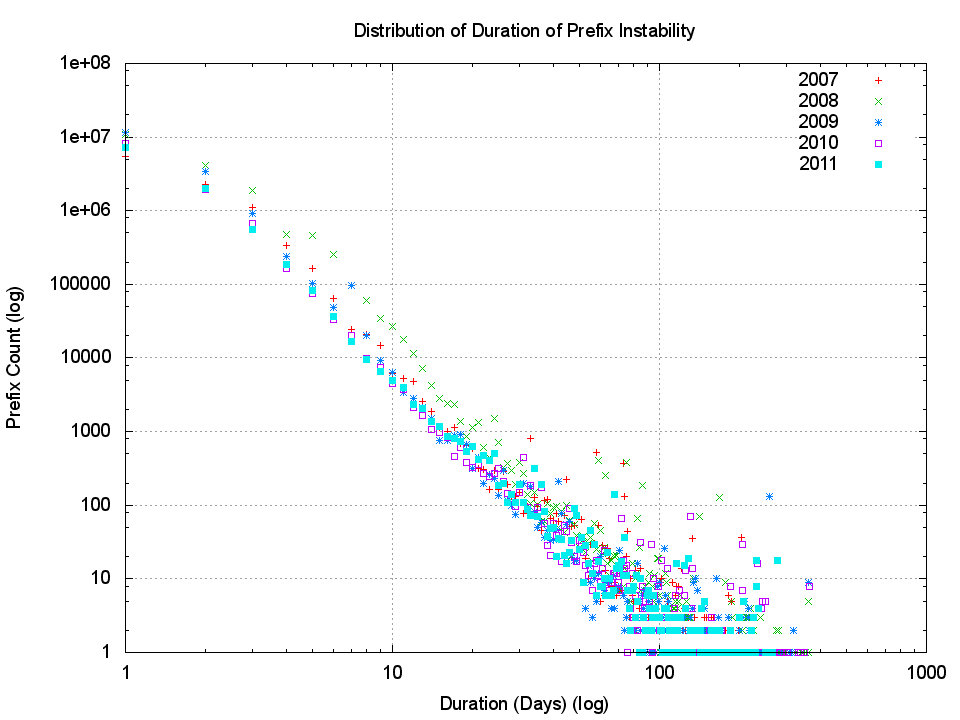
Figure 9 – Distribution of Prefix Instability Duration
Some 10,000 prefixes are unstable for 14 days or longer, while 4,600 prefixes are unstable for 21 days or longer. Only 8 prefixes are unstable every day, which corresponds to the so-called" beacon prefixes that flicker between announced and withdrawn states on an hourly or two-hourly basis as part of a BGP research program. If we are looking for a "core" set of prefixes that are updated every day, then this is not evident in the BGP. Prefixes that are unstable become stable again very quickly, while the set of persistently unstable prefixes is a very small set indeed.
Is this just some strange artifact of AS131072, or do other BGP route collection archives see much the same "flatness"? I won't reproduce the data here, but all the updates collected by the RIPE RIS service and the Route Views archive has been similarly analysed. The graphs of the data can be seen at http://bgp.potaroo.net/bgp-analysis/ris/ for the RIPE Routing Information Service bgp update collection, and http://bgp.potaroo.net/bgp-analysis/rva/ for the Route-Views BGP update archive.
There is evidence of some level of growth in the number of updated prefixes and number of BGP announcements per day, but the rate of growth of these parameters is far lower than the rate of growth of the routing table itself. So it appears that this "flatness" in the metrics of BGP update growth is visible in many parts of the networks, and visible both in networks that are the so-called "Tier 1" transit providers and in the lower tiered edge networks that live at the periphery of the routing galaxy. It appears reasonable to conclude that this is a behavior that is consistent across all of the routing space.
Why is the world of BGP Flat?
There are two components of the dynamic behavior of BGP. The first component is the "originating" prefix instability events that trigger BGP to hunt for a new stable state for that prefix, and the second component is the "amplification" that BGP itself generates in seeking a new stable state. Being a distance vector protocol BGP will continue to generate updates until each BGP speaker reaches a converged state.
Both components of BGP have been scale-free for the past four years at least.
It's possible to explain the second component by examining the topology of the IPv4 network over time.
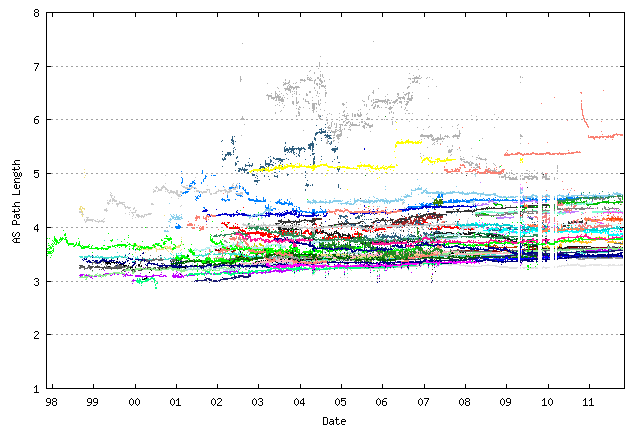
Figure 10 – Average AS Path Length as seen by Route Views peers
As shown in Figure 10, the Internet has been remarkably steady in terms of an average AS Path Length metric for more than 10 years. Over the same extended period the number of routing entries has grown from 50,000 to 300,000 entries, yet the "diameter" of the Internet has remained relatively constant, and all the routing domain growth has increased its "density" of interconnection rather than its radial length. In such an environment BGP has been able to scale very effectively, as the limits to the amount of update traffic required for BGP to reach convergence appears to be more strongly related to the "diameter" of the Internet, in terms of AS hop count, than it is related to the "density" of the Internet, in terms of AS interconnectivity metrics. So a more densely connected Internet that preserves the diameter appears to take the same time to reach convergence as the network grows. It is a reasonably conjecture that a more sparsely connected Internet that extends the diameter of the network as it grows would exhibit increasing convergence times and increasing number of updates to reach convergence, but without radically altering the current arrangements of peering and interconnection in today's Internet this is a challenging conjecture to prove via direct observation!
So when instability occurs, the amount of BGP update traffic to reach convergence appears to be held steady due to the dense interconnectivity of the Internet.
However, this still leaves the question of why the number of instability events is also not growing at the same rate as the routing table. This a topic of current investigation, as there is no immediately obvious reason as to why this set has not been growing at the same rate as the routing table itself.
BGP: Scaling or Failing?
I'm not sure I could say that BGP is on a sure path to perdition, based on the collected data relating to the growth in the routing system and the dynamic behaviour of BGP.
None of the metrics indicate that we are seeing such an explosive level of growth in the routing system that it will fundamentally alter the viability of carrying a complete eBGP routing table in the near future, nor do the characteristics of convergence behaviour show any sign of the Internet entering into a phase of uncontrollable route instability. Indeed it appears that the dynamic load imposed by BGP in terms of computing updates and maintaining a complete routing table imposes the same level of computational load today as it did back in 2004.
So if BGP is going to collapse through overload at some point in the future, then none of the signs of such a dire fate are visible at this stage.
![]()
Disclaimer
The above views do not necessarily represent the views of the Asia Pacific Network Information Centre.
![]()
About the Author
GEOFF HUSTON is the Chief Scientist at APNIC, the Regional Internet Registry serving the Asia Pacific region.